We zoeken de inverse functie van de volgende functie:
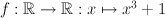
Er bestaan geen verschillende reële getallen a en b waarvoor f(a) = f(b), f is dus injectief. Bovendien is elk reëel getal y te schrijven als x³+1 waarbij x ook een reëel getal is. De functie met voorschrift f(x) = x³+1 bereikt alle reële getallen en is dus eveneens surjectief.
Hierdoor is f bijectief hetgeen garandeert dat de inverse functie bestaat. Om het voorschrift van f-1 te vinden stellen we y = f(x) en keren we de rollen van x en y om, we lossen dan op naar y:
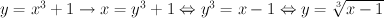
Het domein en codomein van f worden respectievelijk het codomein en domein van f-1. Beide waren echter de reŽle getallen, we vinden dus:
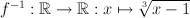
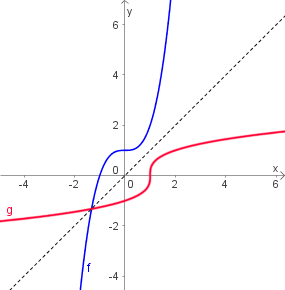
In onderstaande figuur tonen we de grafieken van beide functies, met g = f-1. Als hulplijn is de eerste bissectrice met als vergelijking y = x weergeven. Inverse functies zijn immers spiegelbeelden ten opzicht van deze as.
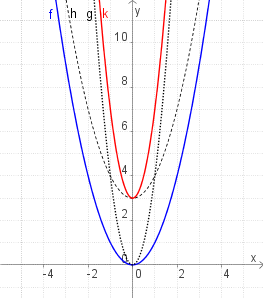
Gegeven is de functie met als voorschrift f(x) = x². Vertrekkend van de grafiek, zoeken we de grafiek van k(x) = f(2x)+3. Deze functie heeft als voorschrift k(x) = (2x)²+3, dus k(x) = 4x²+3.
Ten opzichte van f, hebben we onder andere samendrukking met een factor 2. Dit geeft aanleiding tot een functie g(x) = f(2x).
We hebben ook een verschuiving van de functiewaarden over een afstand 3 naar boven. Hiervoor beschouwen we een functie h(x) = f(x)+3.
Om tot de grafiek van k te komen, kunnen we f samendrukken en vervolgens verschuiven (van f via g naar k) of eerst f verschuiven en vervolgens samendrukken (van f via h naar k). De verschillende grafieken zijn in onderstaande figuur getekend met een rooster om de schalingen en verschuivingen duidelijk te maken.