| opgave | functie | domein | bereik |
|---|---|---|---|
| a | $ y\:=\:x $ | $ \mathbb{R} $ | $ \mathbb{R} $ |
| b | $ y\:=\:x^2 $ | $ \mathbb{R} $ | $ \mathbb{R}^+ $ |
| c | $ y\:=\:x^3 $ | $ \mathbb{R} $ | $ \mathbb{R} $ |
| d | $ y\:=\frac{\:1}{x} $ | $ \mathbb{R}_0 $ | $ \mathbb{R}_0 $ |
| e | $ y\:=\:\left|x\right| $ | $ \mathbb{R} $ | $ \mathbb{R}^+ $ |
| f | $ y\:=\frac{\:1}{\left|x\right|} $ | $ \mathbb{R}_0 $ | $ \mathbb{R}^+_0 $ |
| g | $ y\:=\:x^{-2} $ | $ \mathbb{R}_0 $ | $ \mathbb{R}_0 $ |
| h | $ y\:=\:\sqrt{x} $ | $ \mathbb{R}^+ $ | $ \mathbb{R}^+ $ |
| i | $ y\:=\:\sqrt[3]{x} $ | $ \mathbb{R} $ | $ \mathbb{R} $ |
| j | $ y\:=\:e^x $ | $ \mathbb{R} $ | $ \mathbb{R}^+_0 $ |
| k | $ y\:=\:e^{x-2}+3 $ | $ \mathbb{R} $ | $ \text{]}3,+\infty\text{[} $ |
| l | $ y\:=\:5^x $ | $ \mathbb{R} $ | $ \mathbb{R}^+_0 $ |
| m | $ y\:=\:2^{-x} $ | $ \mathbb{R} $ | $ \mathbb{R}^+_0 $ |
| n | $ y\:=\:2^{-x}-3 $ | $ \mathbb{R} $ | $ \text{]}\:-3,\:+\infty\text{ [} $ |
| o | $ y\:=\:\ln\left(x\right) $ | $ \mathbb{R}_0^+ $ | $ \mathbb{R} $ |
| p | $ y\:=\:\log_{10}\left(x\right) $ | $ \mathbb{R}_0^+ $ | $ \mathbb{R} $ |
| q | $ y\:=\:\log_{10}\left(100^x\right) $ | $ \mathbb{R} $ | $ \mathbb{R} $ |
| r | $ y\:=\:\ln\left(x-2\right)+1 $ | $ \text{] }2,\:+\infty\:\text{[} $ | $ \mathbb{R} $ |
| s | $ y\:=\:\cos\left(x\right) $ | $ \mathbb{R} $ | $ \left[-1,\:1\right] $ |
| t | $ y\:=\:\sin\left(2x\right) $ | $ \mathbb{R} $ | $ \left[-1,\:1\right] $ |
| u | $ y\:=\:-\sin\left(\frac{x}{2}\right) $ | $ \mathbb{R} $ | $ \left[-1,\:1\right] $ |
| v | $ y\:=\:\cos\left(\pi x\right) $ | $ \mathbb{R} $ | $ \left[-1,\:1\right] $ |
| w | $ y\:=\:3\cos\left(2-x\right) $ | $ \mathbb{R} $ | $ \left[-3\:,\:3\right] $ |
| x | $ y\:=\:\sin\left(x-\frac{\pi}{3}\right)+1 $ | $ \mathbb{R} $ | $ \left[0\:,\:2\right] $ |
| y | $ y\:=\frac{\:3}{2}\sin\left(3x\right)+1 $ | $ \mathbb{R} $ | $ \left[-\frac{1}{2}, \frac{5}{2}\right] $ |
| z | $ y=\:\tan\left(x+\frac{\pi}{4}\right) $ | $ \mathbb{R}\backslash\left\{\frac{\:\pi}{4}+k\pi\:\:\text{|}\:k\:\in\mathbb{Z} \right\} $ | $ \mathbb{R} $ |
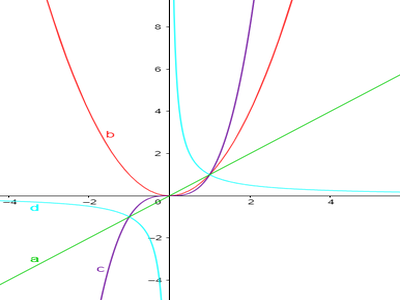
In onderstaande grafiek zijn de functies van a. tot en met d. weergegeven.

In onderstaande grafiek zijn de functies van e. tot en met h. weergegeven.

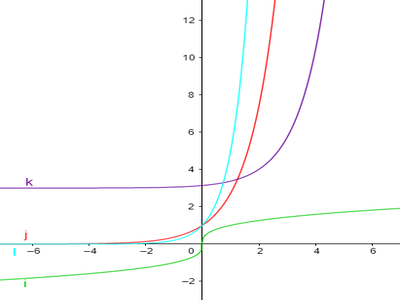
In onderstaande grafiek zijn de functies van i. tot en met l. weergegeven.
In onderstaande grafiek zijn de functies van m. tot en met p. weergegeven.

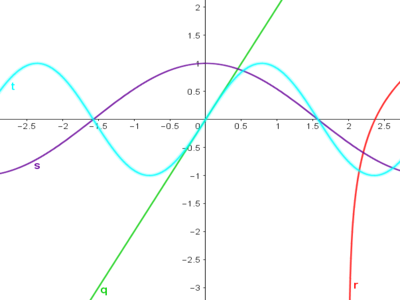
In onderstaande grafiek zijn de functies van q. tot en met t. weergegeven.
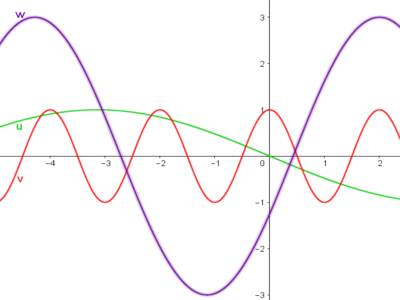
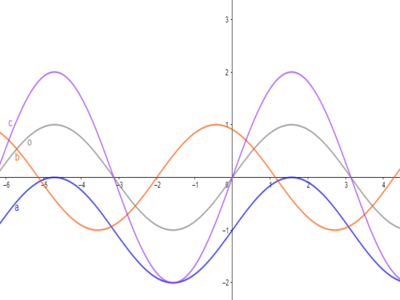
In onderstaande grafiek zijn de functies van u. tot en met w. weergegeven.
In onderstaande grafiek zijn de functies van x. tot en met z. weergegeven.


| a. noch injectief, noch surjectief |
| b. injectief |
| c. surjectief |
| d. bijectief |
| a. $ f^{-1}\left(x\right)\:=\frac{x+4}{2} $ | b. $ f^{-1}\left(x\right)\:=\sqrt{x} $ | c. niet inverteerbaar | d. $ f^{-1}\left(x\right)\:=\sqrt[3]{x-1} $ |
| opgave | $ f\:+\:g $ | $ f\cdot g $ | $ \frac{f}{g} $ | $ g\:\circ\:f\: $ | $ f\:\circ\:g $ |
|---|---|---|---|---|---|
| a | $ \text{[}-1,\:+\:\infty\:\text{[} $ | $ \text{[}-1,\:+\:\infty\:\text{[} $ | $ \text{]}-1,\:+\infty\:\text{[} $ | $ \text{[}-1,\:+\:\infty\:\text{[} $ | $ \text{[}-2,\:+\infty\:\text{[} $ |
| b | $ \left[0,1\right] $ | $ \left[0,1\right] $ | $ \text{[}0\:,\:1\text{[} $ | $ \left[0,1\right] $ | $ \text{]}-\infty,\:1\:\text{]} $ |
| c | $ \mathbb{R}^+ $ | $ \mathbb{R}^+ $ | $ \mathbb{R}_0^+ $ | $ \mathbb{R} $ | $ \mathbb{R}^+ $ |
| d | $ \mathbb{R} $ | $ \mathbb{R} $ | $ \mathbb{R}\backslash\left\{-3,\:3\right\} $ | $ \mathbb{R} $ | $ \mathbb{R} $ |
De functie o ("origineel") stelt steeds f(x) voor. De letters van de andere grafieken corresponderen met de letters van de opgaven.
In onderstaande grafiek zijn de functies van opgaven a. tot en met c. voor f(x) = $x^2$ weergegeven.
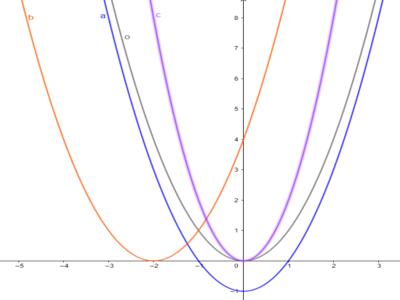
In onderstaande grafiek zijn de functies van opgaven d. tot en met f. voor f(x) = $x^2$ weergegeven.

In onderstaande grafiek zijn de functies van opgaven a. tot en met c. voor f(x) = $\sqrt{x}$ weergegeven.
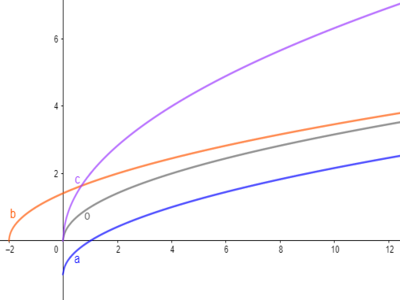
In onderstaande grafiek zijn de functies van opgaven d. tot en met f. voor f(x) = $\sqrt{x}$ weergegeven.
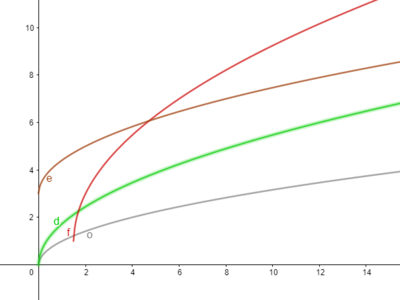
In onderstaande grafiek zijn de functies van opgaven a. tot en met c. voor f(x) = $e^x$ weergegeven.
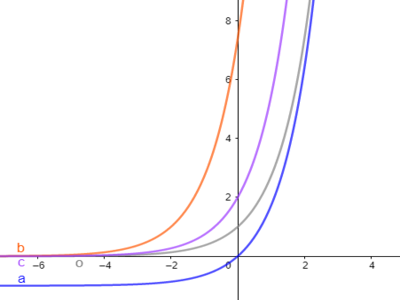
In onderstaande grafiek zijn de functies van opgaven d. tot en met f. voor f(x) = $e^x$ weergegeven.

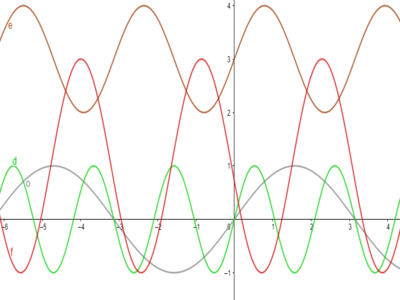
In onderstaande grafiek zijn de functies van opgaven a. tot en met c. voor f(x) = $\sin\left(x\right)$ weergegeven.
In onderstaande grafiek zijn de functies van opgaven d. tot en met f. voor f(x) = $\sin\left(x\right)$ weergegeven.
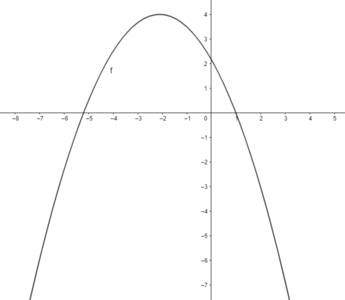
voorschrift: $ y\:=\:-\frac{5}{12}x^2-\frac{7}{4}x+\frac{13}{6} $
vergelijking van de symmetrie-as: $ r\:\longleftrightarrow\:x\:=\:-\frac{b}{2a}=\frac{\frac{\:7}{4}}{2\cdot\left(-\frac{5}{12}\right)}=-\frac{21}{10} $
co$\ddot{o}$rdinaten van de top: $ \left(-\frac{b}{2a},\:f\left(-\frac{b}{2a}\right)\right)\:=\:\left(-\frac{21}{10},\frac{961}{240}\:\right) $
grafiek:
$ \text{y = 3sin}\left(2x-\frac{\pi}{2}\right) $