
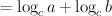
Toepassen van (*) op beide termen

Eigenschap van logaritmen

Opnieuw toepassen van (*)
Er is te bewijzen:
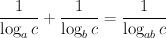
We gebruiken hiervoor eigenschappen van logaritmen uit paragraaf 1.3.5 op pagina 24.
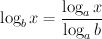
Als we nu a=x nemen, vinden we:
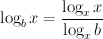
De teller van het rechterlid is 1, dus:

We vertrekken van het linkerlid van de te bewijzen formule:
 |
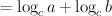 |
Toepassen van (*) op beide termen |
 |
Eigenschap van logaritmen |
|
 |
Opnieuw toepassen van (*) |
We willen de veelterm x³+2x²-5x-6 ontbinden in factoren. Om een eerste factor van de eerste graad te vinden, zoeken we een wortel van de veelterm. Het loont de moeite om de gehele delers van de constante coëfficiënt -6 te proberen, maar met de regel beschreven in paragraaf 1.6.2 op pagina 36 van het boek vinden we dat -1 een wortel is. Bijgevolg is x+1 een factor van de eerste graad. Voor verdere ontbinding in factoren voeren we de deling uit van x³+2x²-5x-6 door x+1 met behulp van de regel van Horner:
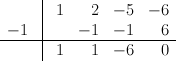
In de onderste rij lezen we het resultaat van de deling af:

Voor de ontbinding van de tweedegraadsveelterm x²+x-6 gebruiken we de formule in paragraaf 1.6.4; we bepalen dus eerst de wortels van deze veelterm met de discriminantformules in paragraaf 1.6.2:
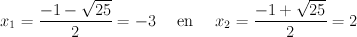
Zo vinden we x²+x-6 = (x+3)(x-2). De ontbinding in factoren van x³+2x²-5x-6 is dus:
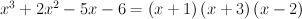
We zoeken alle x-waarden die voldoen aan de ongelijkheden:

Voor het oplossen van de ongelijkheden willen we de leden vermenigvuldigen met de factor x-3. De resulterende ongelijkheden hangen dan af van het teken van x-3 en bijgevolg zoeken we afzondelijk oplossingen met x-3 > 0 en oplossingen met x-3 < 0.
Oplossingen met x-3 > 0:
Voor getallen x met x-3 > 0, dit wil zeggen x > 3, geldt:

Geen enkel getal kan aan deze laatste ongelijkheden voldoen, er zijn dus geen oplossingen met x > 3.
Oplossingen met x-3 > 0:
Voor getallen x met x-3 < 0, dit wil zeggen x < 3, geldt:
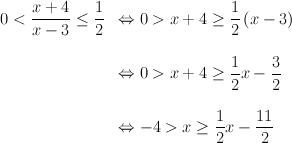
We bekijken nu de ongelijkheden in de laatste regel. Uit de eerste ongelijkheid volgt direct dat x kleiner moet zijn dan -4. We lossen de tweede ongelijkheid op naar x:

We bekomen hiermee een tweede voorwaarde: x moet groter dan of gelijk aan -11 zijn. De oplossingen van de ongelijkheden zijn dus alle getallen x waarvoor:
